Optimization Toolbox
Рекомендуем Вам перейти на Engee – Российскую платформу математических вычислений и динамического моделирования.
Optimization Toolbox предоставляет функции для поиска параметров, которые минимизируют или максимизируют цели при заданных ограничениях. Набор инструментов включает в себя решатели для линейного программирования (LP), смешанного целочисленного линейного программирования (MILP), квадратичного программирования (QP), нелинейного программирования (NLP), метода наименьших квадратов с линейными ограничениями, нелинейного метода наименьших квадратов и решатели для нелинейных уравнений. Вы можете определить свою задачу оптимизации с помощью функций и матриц или путем указания переменных выражений, которые отражают лежащую в основе математику.
Вы можете использовать соответствующие решатели для поиска оптимальных решений непрерывных и дискретных задач, выполнения анализа для выбора компромиссного решения и включать методы оптимизации в алгоритмы и приложения. Инструмент позволяет выполнять задачи оптимизации проектирования, включая оценку параметров, выбор компонентов и настройку параметров. Он может быть использован для поиска оптимальных решений в таких приложениях, как оптимизация портфеля, распределение ресурсов, а также планирование производства.
Определение задач оптимизации
Моделируйте проект или решение задачи как задачу оптимизации. Установите целевые параметры и решения в качестве переменных оптимизации. Используйте их при определении целевой функции для оптимизации с ограничениями для ограничения возможных значений переменных.
Моделирование
Преобразуйте описание задачи в математическую форму путем определения переменных оптимизации, цели и ограничений, чтобы ее можно было решить с помощью методов оптимизации.
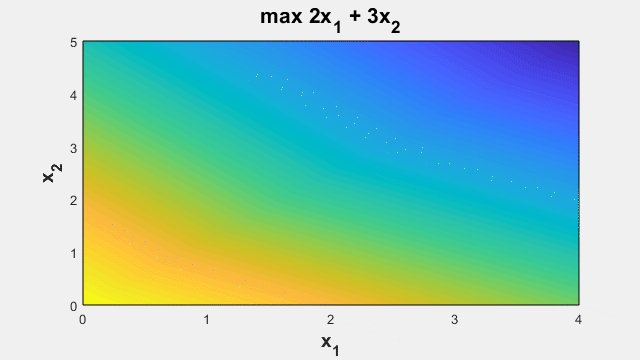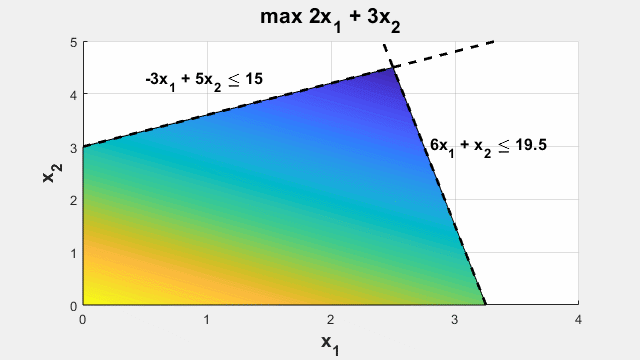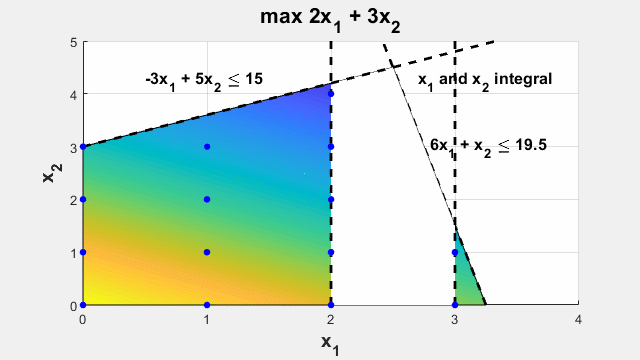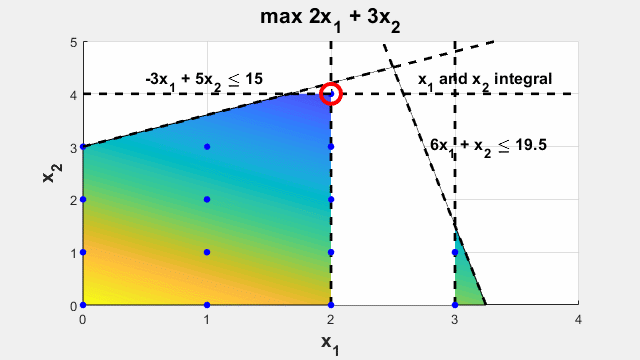
Базовая задача оптимизации
Напишите цель и ограничения в MATLAB, используя выражения, которые отражают математическую форму. Постройте их с помощью переменных оптимизации, математических операторов, матричных операций и функций переменных. Примените автоматически выбранный решатель.
Оптимизация на основе решателей
Напишите цель и ограничения в MATLAB, используя функции, когда используются нелинейные ограничения и коэффициентные матрицы, в случае использования линейных ограничений. Постройте их с матричными операциями MATLAB, математическими операторами и функциями. Примените соответствующий решатель.
Решение задачи оптимизации
Примените решатель к задаче оптимизации, чтобы найти оптимальное решение и задайте набор значений переменных оптимизации, которые находят оптимальное значение целевой функции, если таковые имеются, и отвечают ограничениям, если таковые имеются.
Выбор решателя
Решение с использованием нелинейного, квадратичного, линейного, смешанного целоцисленного, наименьших квадратов или многоцелевого решателя в зависимости от типов задач и ограничений в задаче оптимизации. В базовом подходе решатель выбирается автоматически.
Опции решателя
Задайте параметры оптимизации для настройки процесса оптимизации, например, для выбора алгоритма оптимизации, используемого решателем, или для задания условий завершения. Установите параметры для мониторинга и построения графика процесса оптимизации.
Вывод процесса оптимизации и улучшение результатов
Просмотрите меры оптимальности и итерационное отображение для оценки решения. Используйте ссылки в сообщениях о выходе, чтобы узнать больше. Повышайте производительность в нелинейных задачах путем задания градиентов или использования параллельных вычислений для оценки градиентов.
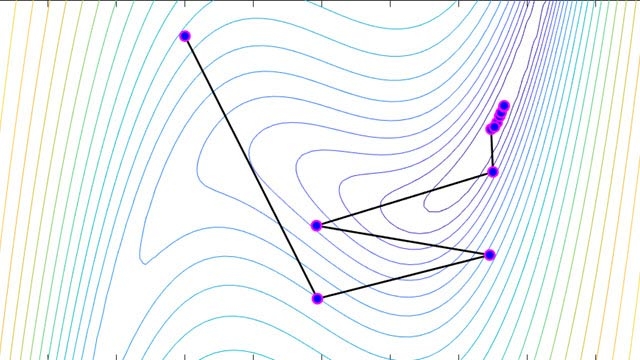
Нелинейное программирование
Решайте оптимизационные задачи, которые имеют нелинейную цель или подвержены нелинейным ограничениям.
Решатели
Примените квази-Ньютоновские (quasi-Newton), доверительной области (trust-region) или симплексные алгоритмы Нелдера-Мида (Nelder-Mead Simplex) для решения задач без ограничений. Применяйте алгоритмы внутренней точки (interior-point), последовательного квадратичного программирования (SQP) или аналитические алгоритмы доверительной области (trust-region-reflective) для решения задач с ограничениями.
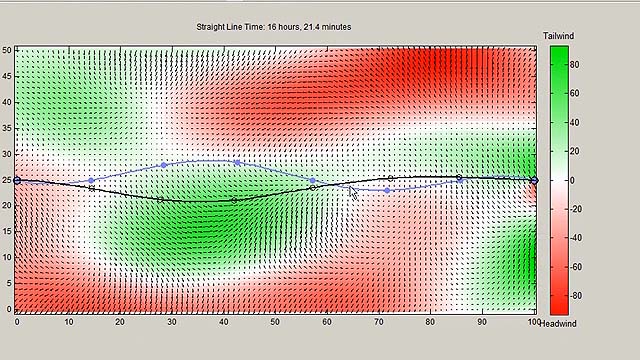
Приложения
Используйте нелинейную оптимизацию для оценки и настройки параметров, поиска оптимальных конструкций, вычисления оптимальных траекторий, построения надежных портфелей и других приложений, где существует нелинейная связь между переменными.
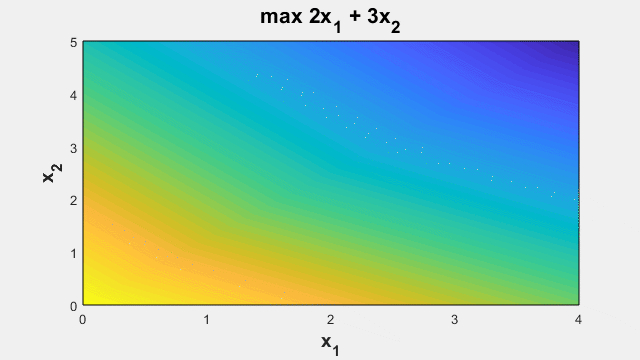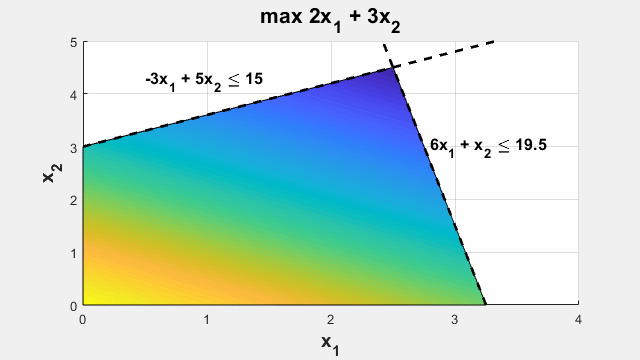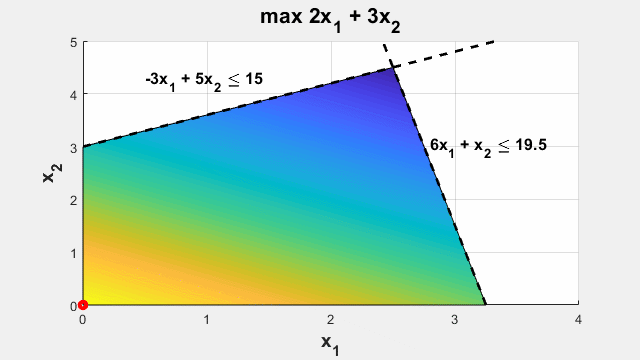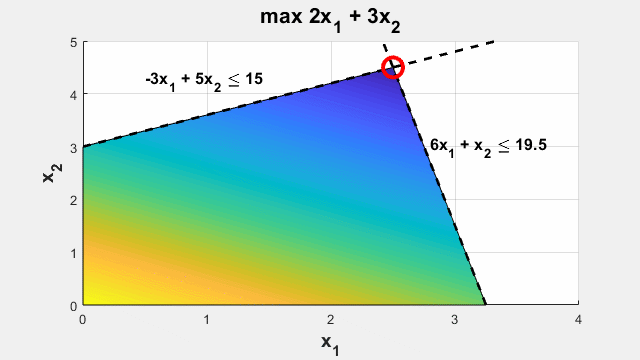
Линейное и квадратичное программирование
Решение оптимизационных задач, имеющих линейные или выпуклые квадратичные целевые функции и подчиняющиеся линейным ограничениям.
Решатели линейного программирования
Для задач линейного программирования применяются алгоритмы двойственного симплекса или внутренней точки.
Решатели квадратичного программирования
Для решения задач квадратичного программирования применяются алгоритмы внутренней точки или доверительной области.
Приложения
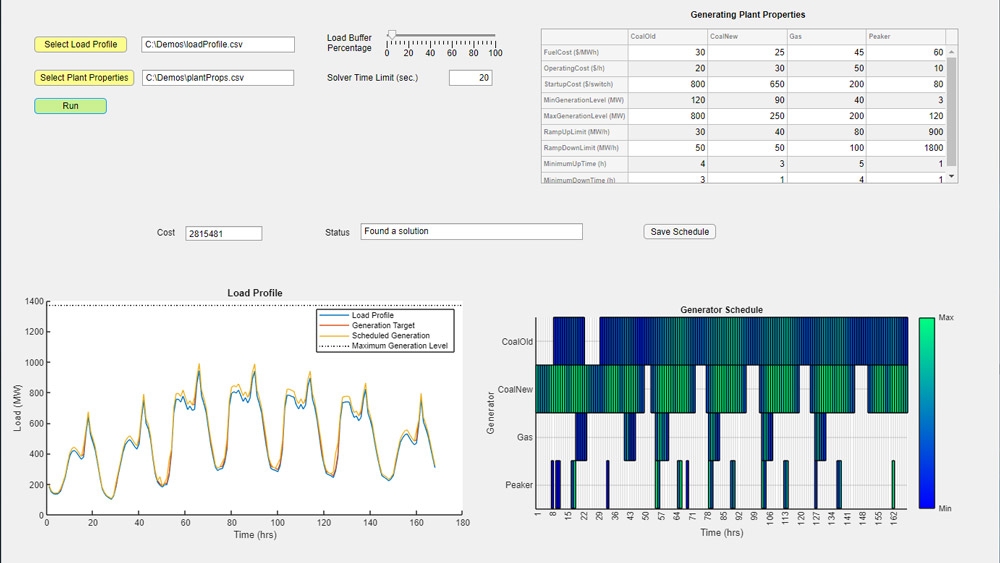
Используйте линейное программирование для таких задач, как распределение ресурсов, планирование производства и планирование инвестиций. Используйте квадратичное программирование для таких задач, как оптимизация проекта, оптимизация портфеля и управление гидроэлектростанциями.
Смешанное целочисленное линейное программирование
Решение задачи оптимизации, которые имеют линейные целевые функции, подчиненные линейным ограничениям, а так же с дополнительным ограничением, что некоторые или все переменные должны быть целочисленными.
Решатели
Решайте задачи смешанного целочисленного линейного программирования с использованием алгоритма ветвей и границ, который включает в себя предварительную обработку, эвристику для генерации допустимых точек и отсекающих плоскостей.
Алгоритмы смешанного целочисленного линейного программирования
Используйте решатель смешанного целочисленного линейного программирования для построения специальных алгоритмов.
Приложения
Модель с целочисленными переменными, когда есть решения вкл/выкл или логические ограничения, а также когда значения переменных должны быть целыми. Задачи маршрутизации, планирования, назначения и составления бюджета предприятия являются типичными приложениями.
Многоцелевая оптимизация
Решайте задачи оптимизации, которые имеют несколько целевых функций, подчиненных набору ограничений.
Решатели
Формулировка задачи должна быть как достижение цели или минимаксное решение. Используйте достижение цели, если для каждой из целей есть дополнительно взвешенные значения целей. Используйте минимакс для минимизации наихудшего значения набора целевых функций.
Приложения
Использование многокритериальной оптимизации при компромиссах, необходимых для двух или более конфликтующих целей. Примерами являются вес и прочность в структурном проектировании либо риск и доходность в оптимизации портфеля.
Метод наименьших квадратов и решение уравнений
Решайте нелинейные задачи методом наименьших квадратов, а также нелинейные системы уравнений с учетом связанных ограничений. Решайте линейные задачи методом наименьших квадратов с учетом границ и линейных ограничений.
Решатели
Применяются методы Левенберга-Марквардта, доверительные регионы или алгоритмы внутренней точки.
Приложения метода наименьших квадратов
Используйте линейные решатели наименьших квадратов для подбора линейной модели к полученным данным или для решения системы линейных уравнений, в том числе когда параметры подчиняются линейным ограничениям и переменные ограничены.
Нелинейный метод наименьших квадратов
Используйте нелинейные решатели наименьших квадратов для подгонки нелинейной модели к полученным данным или для решения системы нелинейных уравнений, в том числе когда на параметры наложены ограничениям.
Развертывание
Разработка и построение инструментов поддержки принятия решений на основе оптимизации. Интеграция с корпоративными системами и развертка алгоритмов оптимизации во встроенных системах.
MATLAB Compiler
Используйте MATLAB Compiler и MATLAB Compiler SDK для развертывания моделей оптимизации MATLAB в виде автономных исполняемых файлов, веб-приложений, общих библиотек C/C++, сборок Microsoft.NET, классов Java и пакетов Python.
 Документация
Документация
 Математическое моделирование с оптимизацией, Часть 1: от описания задачи к математическому программированию (англ.)
Математическое моделирование с оптимизацией, Часть 1: от описания задачи к математическому программированию (англ.) Обзор теории оптимизации
Обзор теории оптимизации