Введение

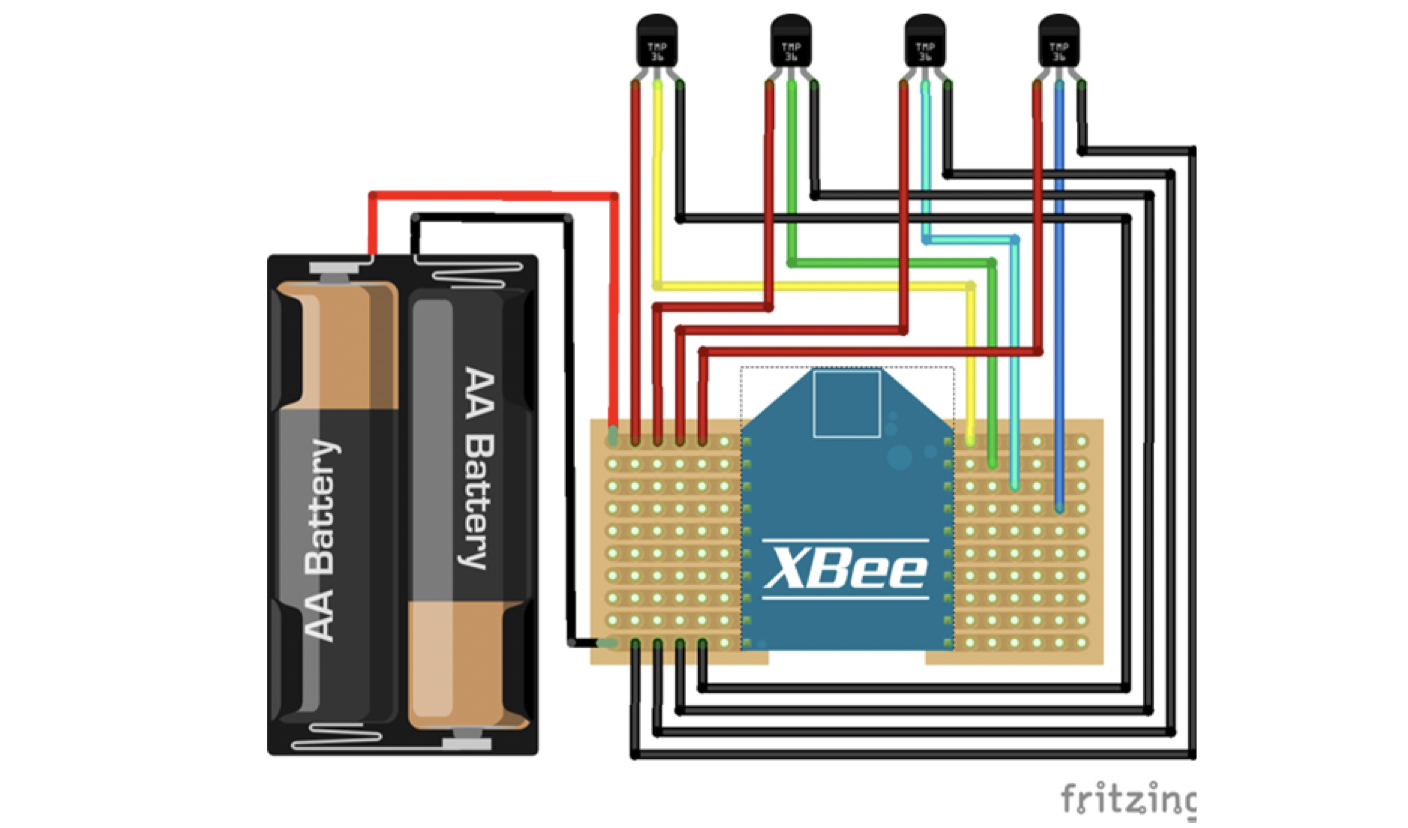
В первом, втором и третьем постах было показано как выгрузить данные из сети XBEE, построить и протестировать такую сеть и откалибровать показания датчиков температуры распределенных по квартире. В этом посте будет показан базовый анализ данных, преследующий две цели:

1. Определение времени нагрева помещения после включения тепла

2. Обнаружение наиболее медленно прогреваемых помещений для регулировки вентилей батарей

Предпросмотр данных

Как упоминалось в предыдущем посте, показания температуры считывались каждые 2 минуты в течении 9 дней. Всего было 14 датчиков: 9 внутри, 2 снаружи и 3 на батареях. Данные сохранены в файле twoweekstemplog.txt, который доступен на File Exchange.

[tempF,ts,location,lineSpecs] = XBeeReadLog('twoweekstemplog.txt',60);

tempF = calibrateTemperatures(tempF);

plotTemps(ts,tempF,location,lineSpecs)

legend('off')

xlabel('Date')

title('All Data Overview')

Рисунок 1. Вся измеренная температура за 9 дней

Видно, что график замусорен и плохо читается. Поэтому уберем с него данные по батареям и легенду:

notradiator = [1 2 3 5 6 7 8 9 10 12 13];

plotTemps(ts,tempF(:,notradiator),location(notradiator),lineSpecs(notradiator,:))

legend('off')

xlabel('Date')

title('All Inside and Outside Temperature Data')

Рисунок 2. Температура в помещении и на улице без температуры батарей

Теперь видно, что один из датчиков температуры, расположенных на улице (синяя линя) выдавал ошибочные данные. Поэтому надо удалить ошибочные данные. Так как данные собирались в марте в штате Массачусетс, то можно предположить, что температура воздуха была не более 80F (26.6С). Все показания датчика, превышающие это значение должны быть заменены на NaN (Not-a-Number), для исключения из последующего анализа:

outside = [3 10];

outsideTemps = tempF(:,outside);

toohot = outsideTemps>80;

outsideTemps(toohot) = NaN;

tempF(:,outside) = outsideTemps;

plotTemps(ts,tempF(:,notradiator),location(notradiator),lineSpecs(notradiator,:))

legend('off')

xlabel('Date')

title('Cleaned-up Inside and Outside Temperature Data')

Рисунок 3. Корректные измерения температуры

Так же будут удалены показания всех, кроме одного, датчиков, расположенных в комнате, а оставшимся датчикам будет дано более краткое имя, что бы график был более читаемым:

show = [1 5 9 12 10 3];

location(show) = ...

{'Bedroom','Kitchen','Living Room','Office','Front Porch','Side Yard'}';

plotTemps(ts,tempF(:,show),location(show),lineSpecs(show,:))

ylim([0 90])

legend('Location','SouthEast')

xlabel('Date')

title('Summary of Temperature Data')

Рисунок 4. Показания одного датчика температуры в каждом размещении

Теперь график выглядит намного лучше. Данные собирались в течении 9 дней, и первое, что бросается в глаза – это периодичность значений температуры вне квартиры, с пиками около полудня каждый день. Так же виден пик в придомовом дворике (зеленая линия), происходящий каждый день. Крыльцо расположено на северной стороне квартиры и редко освещается солнцем. Дворик расположен на восточной стороне квартиры, и выброс, скорее всего, соответствует моменту, когда солнечный свет падает прямо на датчик.

Когда начинается нагрев батарей?

Показания датчиков на батареях могут использованы для определения времени, за которое нагреются бойлер и батареи после включения. Сначала, посмотрим на измерения температуры батареи в гостиной за один день:

% Извлечем показания температуры батареи в гостиной (столбец 11) из матрицы |tempF|.

radiatorTemp = tempF(:,11);

% Fill in any missing values:

validts = ts(~isnan(radiatorTemp));

validtemp = radiatorTemp(~isnan(radiatorTemp));

nants = ts(isnan(radiatorTemp));

radiatorTemp(isnan(radiatorTemp)) = interp1(validts,validtemp,nants);

% Построим график

oneday = [ts(1) ts(1)+1];

figure

plot(ts,radiatorTemp,'k.-')

xlim(oneday)

xlabel('Time')

ylabel('Radiator Temperature (\circF)')

title('Living Room Radiator Temperature')

datetick('keeplimits')

snapnow

Рисунок 5. Температура батареи в гостиной за 1 день

Как и ожидалось, можно увидеть резкое повышение температуры батареи с дальнейшим небольшим понижением (когда температура батареи выходит за измеряемый диапазон), а затем постепенное остывание батареи. Наложим на предыдущий график скорость изменения температуры:

tempChange = diff([NaN; radiatorTemp]);

hold on

plot(ts,tempChange,'b.-')

legend({'Temperature', 'Temperature Change'},'Location','Best')

Рисунок 6. График из Рис 5 и с графиком изменения температуры

Можно обнаружить эти пики, выполняя поиск больших скачков температуры. После нескольких попыток обнаружения, были сформулированы следующие критерии нагрева:

1. Температура изменилась больше чем в 4 раза по сравнению с предыдущим изменением температуры

2. Температура изменилась более, чем на 1 градус

3. Оставить первую в последовательности совпадающих точек (удалить дубли)

fourtimes = [tempChange(2:end)>abs(4*tempChange(1:end-1)); false];

greaterthanone = [tempChange(2:end)>1; false];

heaton = fourtimes & greaterthanone;

doubles = [false; heaton(2:end) & heaton(1:end-1)];

heaton(doubles) = false;

Проверим, насколько хорошо обнаруживаются пики, отмечая время обнаружения красной точкой:

figure

plot(ts,radiatorTemp,'k.-')

hold on

plot(ts(heaton),radiatorTemp(heaton),'r.','MarkerSize',20)

xlim(oneday);

datetick('keeplimits')

xlabel('Time')

ylabel('Radiator Temperature (\circF)')

title('Heat On Event Detection')

legend({'Temperature', 'Heat On Event'},'Location','Best')

Рисунок 7. Температура батареи. Начало нагрева отмечено красными точками

Видно, что обнаружение корректное, что означает, что теперь можно получить времена начала обогрева квартиры:

heatontimes = ts(heaton);

Насколько быстро происходит нагрев?

Исследуемый термостат – программируемый как «5-на-2», то есть можно запрограммировать его поведение во время рабочих дней и во время выходных. Ночью термостат устанавливается на 62F (16.6С), и на 68F (20С) в 6:15 по будням или в 10:00 по выходным. Эта информация была использована для определения задержки между активацией термостата и нагревом батарей. Сначала требуется создать вектор из всех дней периода тестирования. Понедельник был удален, так как термостат был заранее включен вручную:

mornings = floor(min(ts)):floor(max(ts));

mornings(2) = []; % Remove Monday

Затем было добавлено время (6:15 или 10:00) в зависимости от того был это будний или выходной день:

isweekend = weekday(mornings) == 1 | weekday(mornings) == 7;

mornings(isweekend) = mornings(isweekend)+10/24; % 10:00 AM

mornings(~isweekend) = mornings(~isweekend)+6.25/24; % 6:15 AM

Next I looked for the first time the heat came on after the programmed time each morning.

heatontimes_mat = repmat(heatontimes,1,length(mornings));

mornings_mat = repmat(mornings,length(heatontimes),1);

timelag = heatontimes_mat - mornings_mat;

timelag(timelag<=0) = NaN;

[delay, heatind] = min(timelag);

delay = round(delay*24*60);

Проверим, что найденные времена – правильные. На этом графике, первое время нагрева обведено синим кругом и синие вертикальные линии обозначают включение термостата каждое утро:

heatontemp = radiatorTemp(heaton);

onemorning = mornings(3)+[-1/24 5/24];

figure

plot(ts,radiatorTemp,'k.-')

hold on

plot(heatontimes,heatontemp,'r.','MarkerSize',20)

plot(heatontimes(heatind),heatontemp(heatind),'bo','MarkerSize',10)

plot([mornings;mornings],repmat(ylim',1,length(mornings)),'b-');

xlim(onemorning);

datetick('keeplimits')

xlabel('Time')

ylabel('Radiator Temperature (\circF)')

title('Detection of Scheduled Heat On Events')

legend({'Temperature', 'Heat On Event', 'Scheduled Heat On Event',...

'Scheduled Event'},'Location','Best')

Рисунок 8. Температура батареи за 6 часов. Синяя линия - момент включения нагрева, синим кругом обозначено начало нагрева батареи

Посмотрим на гистограмму задержек:

figure

hist(delay,min(delay):max(delay))

xlabel('Minutes')

ylabel('Frequency')

title('How long before the radiator starts to warm up?')

Рисунок 9. Гистограмма задержек между началом обогрева и началом нагрева батарей

Видно, что задержка между утренним включением термостата и началом нагрева батарей может быть от 7 до 24 минут, но в среднем составляет 12-13 минут.

heatondelay = 12;

Сколько времени занимает нагрев батарей?

После начало нагрева батарей требуется некоторое время для достижения необходимой температуры. Что бы узнать эту задержку требуется искать такое время, при котором температура батареи в первый раз выйдет за пределы измерений после того, как температура была ниже порога в течение 10 минут (5 отсчетов):

maxtemp = max(radiatorTemp);

radiatorhot = radiatorTemp(6:end)==maxtemp & ...

radiatorTemp(1:end-5)

radiatorTemp(2:end-4)

radiatorTemp(3:end-3)

radiatorTemp(4:end-2)

radiatorTemp(5:end-1)

radiatorhot = [false(5,1); radiatorhot];

radiatorhottimes = ts(radiatorhot);

Посмотрим на результаты:

figure

plot(ts,radiatorTemp,'k.-')

hold on

plot(ts(heaton),radiatorTemp(heaton),'r.','MarkerSize',20)

plot(ts(radiatorhot),radiatorTemp(radiatorhot),'b.','MarkerSize',20)

xlim(onemorning);

datetick('keeplimits')

xlabel('Time')

ylabel('Radiator Temperature (\circF)')

title('Radiator Hot Event Detection')

legend({'Temperature', 'Heat On Event', 'Radiator Hot Event'},...

'Location','Best')

Рисунок 10. Значения температуры за 6 часов. Красные точки - время начала обогрева, синие - время достижения батареей максимальной температуры

Выровняем radiatorhottimes относительно heatontimes, используя тот же поход, что и ранее:

radiatorhottimes_mat = repmat(radiatorhottimes',length(heatontimes),1);

heatontimes_mat = repmat(heatontimes,1,length(radiatorhottimes));

timelag = radiatorhottimes_mat - heatontimes_mat;

timelag(timelag<=0) = NaN;

[delay, foundmatch] = min(timelag);

delay = round(delay*24*60);

Гистограмма задержек:

figure

hist(delay,min(delay):2:max(delay))

xlabel('Minutes');

ylabel('Frequency')

title('How long does the radiator take to warm up?')

Рисунок 11. Распределение значений времени, требуемого для нагрева батарей

Видно, что батареям требуется от 4 до 8 минут, чтобы полностью нагреться.

radiatorheatdelay = 6;

В последующем анализе будут использованы только те временные метки, при которых нагрев происходил полностью. Эти данные будут сохранены в векторе heaton:

heatonind = find(heaton);

heatonind = heatonind(foundmatch);

heaton = false(size(heaton));

heaton(heatonind) = true;

Когда остывают батареи?

Тот же самый подход будет использован для того, что бы обнаружить остывание батарей, что бы узнать, когда был выключен нагрев.

heatoff = radiatorTemp(1:end-5)==maxtemp & ...

radiatorTemp(2:end-4)

radiatorTemp(3:end-3)

radiatorTemp(4:end-2)

radiatorTemp(5:end-1)

radiatorTemp(6:end)

heatoff = [heatoff; false(5,1)];

heatofftimes = ts(heatoff);

heatoffind = find(heatoff);

Посмотрим на времена включения нагрева, нагрева батареи и отключения нагрева на едином графике:

figure

plot(ts,radiatorTemp,'k.-')

hold on

plot(ts(heaton),radiatorTemp(heaton),'r.','MarkerSize',20)

plot(ts(radiatorhot),radiatorTemp(radiatorhot),'b.','MarkerSize',20)

plot(ts(heatoff),radiatorTemp(heatoff),'g.','MarkerSize',20)

xlim(onemorning);

datetick('keeplimits')

xlabel('Time')

ylabel('Radiator Temperature (\circF)')

title('Radiator Cooling Event Detection')

legend({'Temperature', 'Heat On Event', 'Radiator Hot Event',...

'Radiator Cooling Event'},'Location','Best')

Рисунок 12. Температура батареи за 6 часов, красные точки - начало нагрева, синие - достижение максимальной температуры, зеленые - начало остужения

За какое время нагревается комната?

Теперь, когда известно, что между включением термостата и началом нагрева проходит примерно 12-13 минут и еще 4-8 минут перед полным нагревом батарей, посмотрим за сколько времени прогревается комната. Пока рассмотрим только прогрев гостиной.Сначала, извлечем нужные данные из матрицы tempF:

livingroomtemp = tempF(:,9);

Let’s look at one day’s worth of living room inside temperatures to see how they compare the the living room radiator temperatures.

Рассмотрим измерения температуры в гостиной за один день и сравним их с температурой батареи в гостиной:

figure

[ax,p1,p2] = plotyy(ts,radiatorTemp,ts,livingroomtemp);

set(ax,'XLim',oneday)

set(ax(1),'YColor','k','YLim',[60 180],'YTick',60:20:180)

set(ax(2),'YColor','b','YLim',[60 72],'YTick',60:2:72,'XTick',[])

set(p1,'Color','k')

set(p2,'Color','b')

datetick(ax(1),'keeplimits')

xlabel(ax(1),'Time')

ylabel(ax(1),'Radiator Temperature (\circF)')

ylabel(ax(2),'Room Temperature (\circF)')

title('Living Room and Radiator Temperatures')

legend([p1,p2],{'Radiator Temperature','Room Temperature'},'Location','SouthEast')

Рисунок 13. Наложение графиков температур батарей и воздуха в гостиной, с различным масштабом оси Y

Как и ожидалось, при повышении температуры батарей повышается и температура в гостиной, но с какой скоростью? Для этого, сначала сегментируем показания температуры по временам, когда начался обогрев. Оставим только возрастающую часть сегментов (до первого максимума температуры в сегменте или до тех пор, пока нагрев не выключен). Так же будем отслеживать максимальную и минимальную температуры в сегментах, и их время. Проинициализируем матрицу для хранения сегментов (segmentTemps), так, чтобы сегменты длиной меньше, чем максимальная были заполнены значением NaN:

numSegments = sum(heaton);

segmentSizes = heatoffind-heatonind+1;

segmentTemps = NaN(numSegments, max(segmentSizes));

for c = 1:numSegments

segmentTemps(c,1:segmentSizes(c)) =

livingroomtemp(heatonind(c):heatoffind(c));

[segmentMaxTemp(c,1),segmentTimeToMax(c,1)] = max(segmentTemps(c,:));

[segmentMinTemp(c,1),segmentTimeToMin(c,1)] =

min(segmentTemps(c,1:segmentTimeToMax(c)));

segmentTemps(c,segmentTimeToMax(c)+1:end) = NaN;

end

% Clip off columns that are all NaN at the end of the matrix.

maxSegmentSize = max(segmentTimeToMax);

segmentTemps = segmentTemps(:,1:maxSegmentSize);

% Shift from 1-based indexes to 0-based minutes.

segmentTimeToMin = (segmentTimeToMin - 1)*2;

segmentTimeToMax = (segmentTimeToMax - 1)*2;

segmentTimes = (0:(maxSegmentSize-1))*2; % Time since heat came on in minutes

Рассмотрим один из сегментов:

figure

plot(segmentTimes, segmentTemps(1,:),'b.-')

hold on

plot(segmentTimeToMin(1),segmentMinTemp(1),'r.','MarkerSize',20)

legend({'Temperature','Minimum Temperature'},'Location','NorthWest')

xlabel('Minutes since radiator started to warm')

ylabel('Temperature (\circF)')

title('Room Temperature During One Heating Event')

Рисунок 14. Температура в комнате за один цикл нагрева, нулевое время - начало нагрева батареи

На графике видно, что температура понижается в течении нескольких минут, а затем повышается почти линейно. Исходя из этого, сместим график так, чтобы начало возрастания температуры было в нуле по оси Y:

figure

plot(segmentTimes-segmentTimeToMin(1),

segmentTemps(1,:)-segmentMinTemp(1),'b.-')

legend({'Temperature Increase'},'Location','NorthWest')

xlabel('Minutes since minimum temperature')

ylabel('Temperature Increase (\circF)')

title('Shifted Room Temperature During One Heating Event')

Рисунок 15. Температура в комнате за один цикл нагрева, смещенная

Теперь отмасштабируем этот сдвиг на все сегменты, так что бы минимальная температура была в нуле по оси Y. Пометим красными точками максимальную температуру в каждом сегменте. Сначала, сместим все времена, основываясь на segmentTimeToMin:

segmentTimes_mat = repmat(segmentTimes,length(segmentTimeToMin),1);

segmentTimeToMin_mat = repmat(segmentTimeToMin,1,length(segmentTimes));

segmentTimesShifted = segmentTimes_mat - segmentTimeToMin_mat;

Затем, сместим все температуры, основываясь на segmentMinTemp:

segmentMinTemp_mat = repmat(segmentMinTemp,1,size(segmentTemps,2));

segmentTempsShifted = segmentTemps - segmentMinTemp_mat;

И найдем полное изменение температуры и его время для каждого сегмента:

segmentRiseTime = segmentTimeToMax-segmentTimeToMin;

segmentTempRise = segmentMaxTemp-segmentMinTemp;

И, наконец, построим график:

figure

h1 = plot(segmentTimesShifted',segmentTempsShifted','b-');

legend(h1(1),{'Temperature Increase'},'Location','NorthWest')

xlim([-10 max(segmentTimesShifted(:))])

xlabel('Minutes since minimum temperature')

ylabel('Temperature Increase (\circF)')

title('Shifted Room Temperature During All Heating Events')

Рисунок 16. Изменение температуры помещения за все циклы нагрева, смещенное

И хотя график выглядит неидеально, можно предположить линейную зависимость. Так как интерес представляет время уставки желаемой температуры (которую можно рассматривать как «теплоемкость» комнаты), перестроим график, так что бы время было осью Y, а температура – осью X («перевернем» оси). Дополнительно, выведем не линейный, а точечный график, чтобы отобразить данные, которые будут аппроксимированы:

% Remove temperatures occuring before the minimum temperature.

segmentTempsShifted(segmentTimesShifted<0) = NaN;

figure

h1 = plot(segmentTempsShifted',segmentTimesShifted','k.');

xlabel('Temperature Increase (\circF)')

ylabel('Minutes since minimum temperature')

title('Time to Heat Living Room')

snapnow

Рисунок 17. Время, требуемое для нагрева гостиной (оси Рис. 16 поменяны местами)

Теперь, выведем уравнение для температуры в гостиной через аппроксимацию данных. Сначала соберем все данные о времени и температуры в один вектор-столбец и удалим NaN:

allTimes = segmentTimesShifted(:);

allTemps = segmentTempsShifted(:);

allTimes(isnan(allTemps)) = [];

allTemps(isnan(allTemps)) = [];

Then I can fit a line to the data.

linfit = polyfit(allTemps,allTimes,1);

Let’s see how well we fit the data.

hold on

h2 = plot(xlim,polyval(linfit,xlim),'r-');

linfitstr = sprintf('Linear Fit (y = %.1f*x + %.1f)',linfit(1),linfit(2));

legend([ h1(1), h2(1) ],{'Data',linfitstr},'Location','NorthWest')

Рисунок 18. Линия аппроксимации значений времени (см. Рис 17)

Видно, что аппроксимация получилась достаточно точной. При рассмотрении коэффициентов аппроксимирующей прямой видно, что между нагревом батарей и повышением температуры в комнате проходит около 3 минут. После этого требуется еще примерно 5 минут что бы нагреть воздух на 1 градус.

Какая комната нагревается дольше всего?

Отмасштабируем анализ на другие комнаты, чтобы узнать, какая же комната нагревается дольше всего. Вышеприведенный код был помещен в функцию temperatureAnalysis, затем полученная функция была применена для каждого датчика внутри комнат:

inside = [1 5 9 12];

figure

xl = [0 14];

for s = 1:size(inside,2)

linfits(s,1:2) = temperatureAnalysis(tempF(:,inside(s)), heaton, heatoff);

y = polyval(linfits(s,1:2),xl) + heatondelay;

plot(xl, y, lineSpecs{inside(s),1}, 'Color',lineSpecs{inside(s),2},...

'DisplayName',location{inside(s)})

hold on

end

legend('Location','NorthWest')

xlabel('Desired temperature increase (\circF)')

ylabel('Estimated minutes to heat')

title('Estimated Time to Heat Each Room')

Рисунок 19. Оценка времени, требуемого для нагрева каждого помещения в квартире

В самом первом посте, было упомянуто, что “несмотря на то, что термостат показывает необходимые 73F, в кабинете спальне холодно.” Учитывая, что термостат находится в гостиной, данные подтверждают забавное наблюдение: кабинет и спальня нагреваются в 2 раза дольше, чем гостиная, а кухня, в свою очередь, немного быстрее.

Заключение

Серия постов началась с намерения использовать беспроводную сеть датчиков температуры на основе XBee для того, чтобы лучше понять за сколько времени прогревается квартира и использовать это знание для подстройки системы отопления для равномерного прогрева.

Вышеприведенный анализ – это только начало анализа, который может быть проведен над собранными данными, но и его уже достаточно для того, чтобы подстроить систему отопления. Можно приоткрыть краны на батареях в кабинете и спальне, и, возможно, прикрыть краны на батареях в гостиной и кухне. Затем будет необходимо собрать данные заново и оценить изменения.

Теперь известно, что между началом работы системы отопления и началом нагрева комнат проходит от 15 до 20 минут и в лучшем случае, температура повысится на 1 градус за 3-5 минут. Термостат запрограммирован так, чтобы поддерживать 62F ночью и нагревать квартиру до 68F утром. Исходя из анализа, термостат должен включаться на 30-40 минут раньше, чтобы успеть обеспечить желаемую температуру. Неудивительно, что счета за тепло будут огромными

Скачать код

Публикации по данной теме:

Постоянное наблюдение за температурой при помощи беспроводной сети датчиков. Часть 1

Постоянное наблюдение за температурой при помощи беспроводной сети датчиков. Часть 2

Постоянное наблюдение за температурой при помощи беспроводной сети датчиков. Часть 3